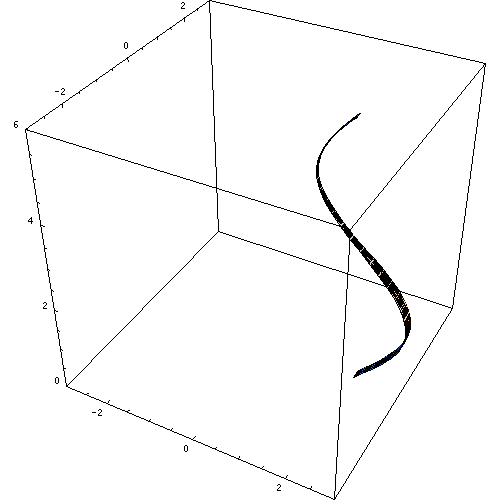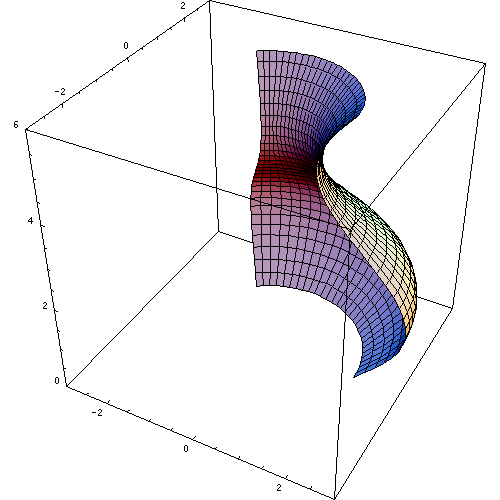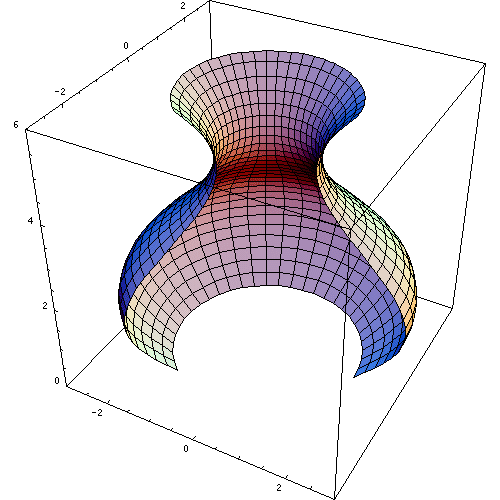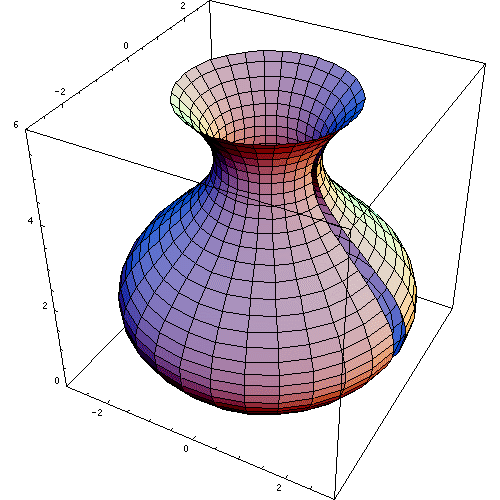
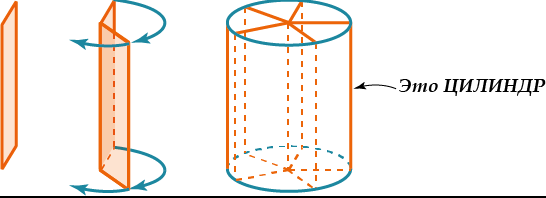
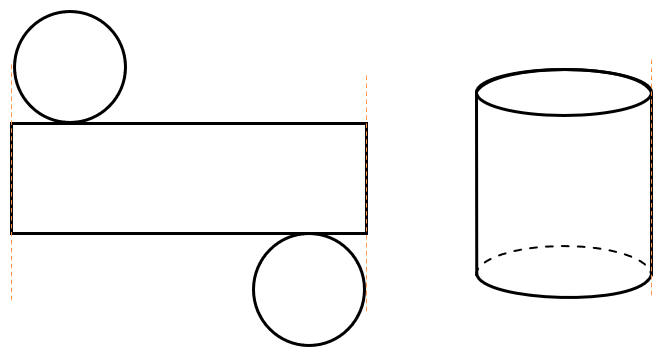
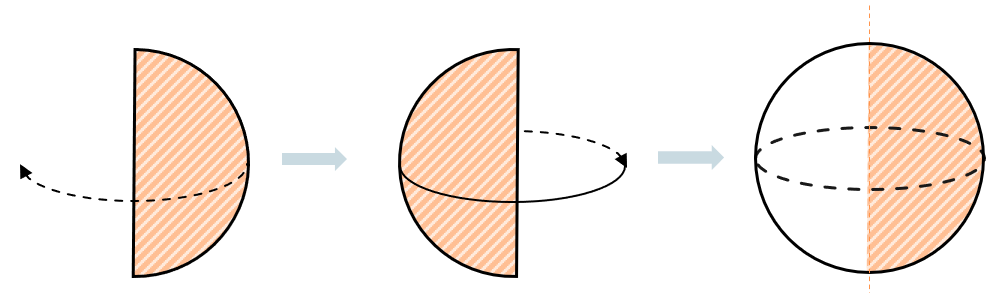
К телам вращения принадлежит
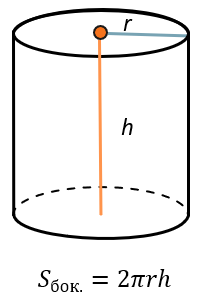
Объем тела вращения вокруг оси Ox, Oy
Категория: Математика. Похожие презентации:. Тела вращения.



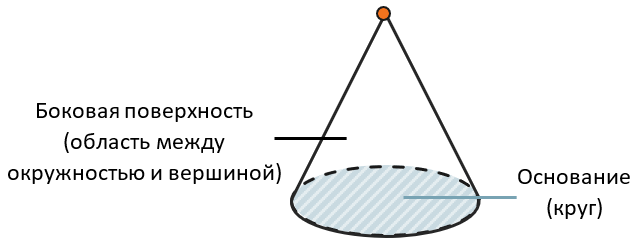


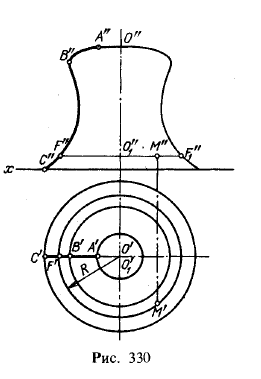

Сформулированы Паппом Александрийским доказательства он не привёл. Первое известное доказательство принадлежит Паулю Гульдину [1]. Площадь поверхности тела, образованного вращением плоской линии замкнутой или незамкнутой вокруг оси, лежащей в плоскости этой линии и не пересекающей её, равна произведению длины вращающейся линии на длину окружности, радиусом которой служит расстояние от оси до барицентра линии [2] [3]. Объём тела, образованного вращением плоской фигуры вокруг оси, расположенной в той же плоскости и не пересекающей фигуру, равен площади фигуры, умноженной на длину окружности, радиусом которой служит расстояние от оси вращения до барицентра фигуры [2] [4]. Пусть в плоскости по одну сторону от прямой расположено несколько материальных точек одинаковой массы. Доказательство : Докажем лемму методом математической индукции.




Презентации задач, программа PowerPoint Ссылки на видео помогут вам понять замысел автора. Вы можете предлагать ученикам задачи для самоподготовки с последующей публикацией ссылок на решение. Презентации можно использовать на уроках. Если у Вас или у ваших учеников есть интересные идеи, можете написать в комментариях.