Как сделать гексаэдр из бумаги схема

Геометрические фигуры
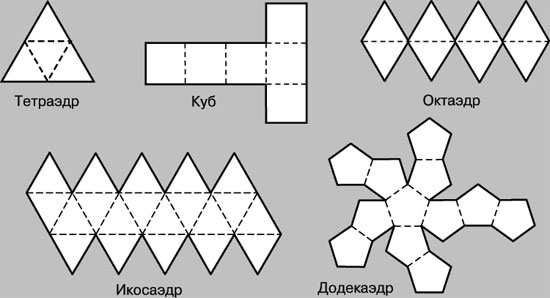
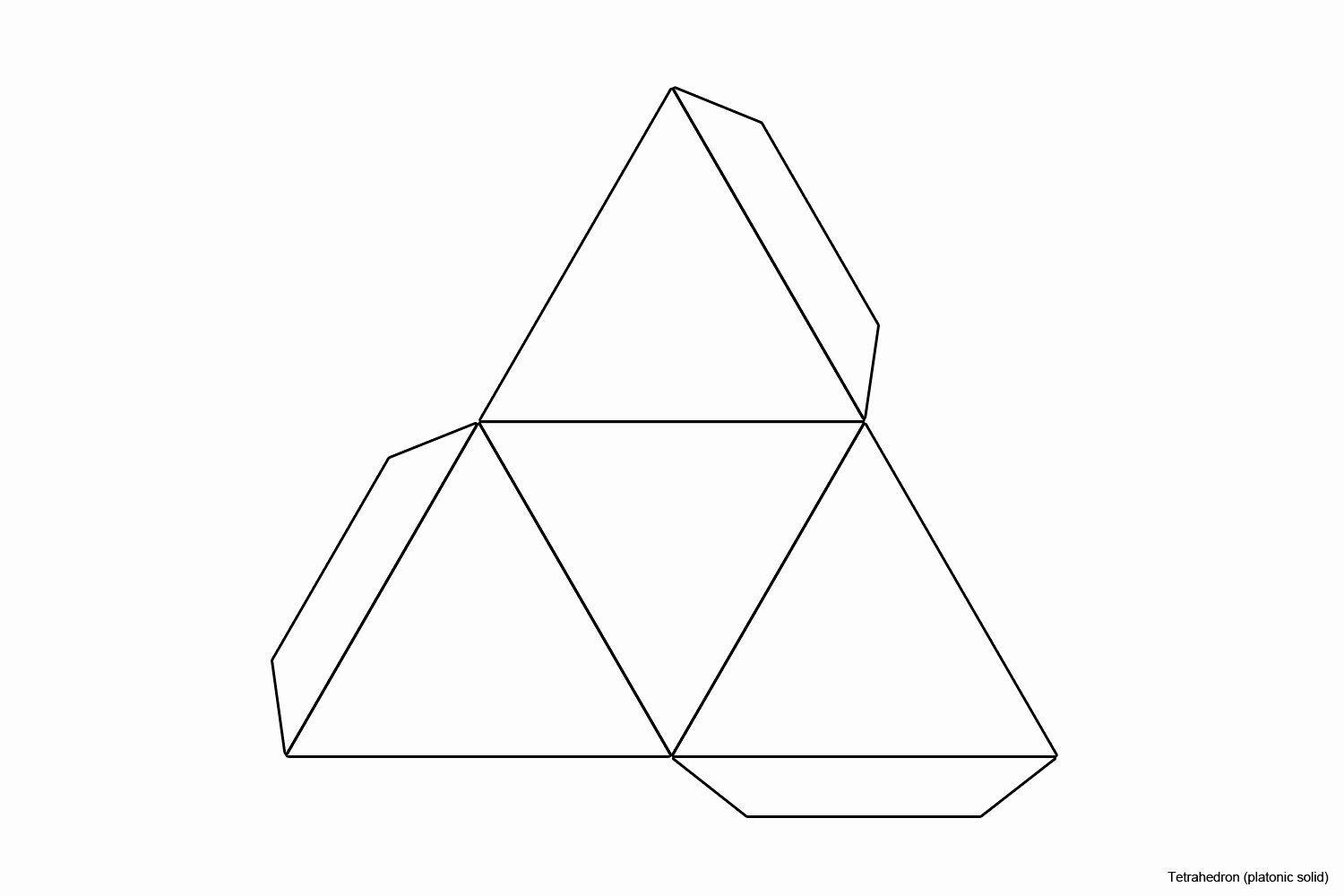
Шаблоны многогранников из бумаги для склеивания. Можно распечатать Платоновы тела бесплатно, скачав напрямую из статьи. Понятие многогранников дети узнают при изучении геометрии в школе.










Одним из самых популярных направлений в оригами является 3D-моделирование. Создание объемных фигур захватывает внимание не только детей, но и взрослых. Если вы уже освоили простейшие схемы и техники и научились делать хотя бы куб из бумаги, можно переходить к более сложным моделям. Лучше всего практиковаться в создании так называемых "Платоновых тел". Их всего пять: тетраэдр, икосаэдр, гексаэдр, додекаэдр и октаэдр. Все фигуры представляют собой правильные многогранники, в основе которых лежат простейшие геометрические фигуры.
- Шаблоны многогранников (Платоновы тела) для распечатывания
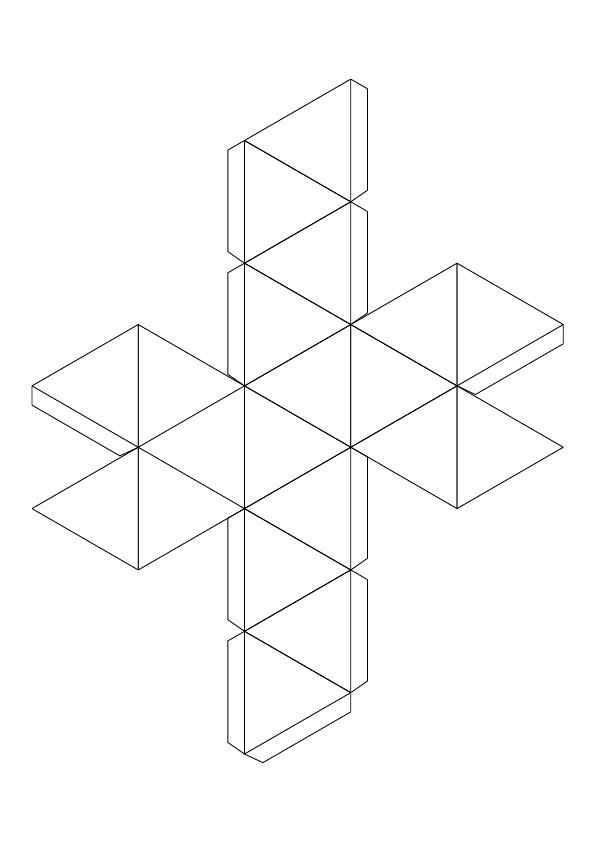
- Для развёртки икосаэдра необходимо 2 листа двухстороннего цветного картона формата А4 или плотной бумаги.
- Рисунки » Трафареты » Трафарет объемный куб.
- Извините, но Livemaster.
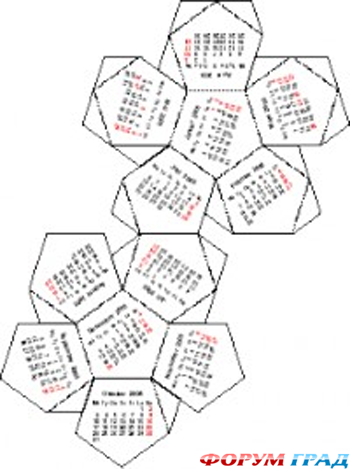
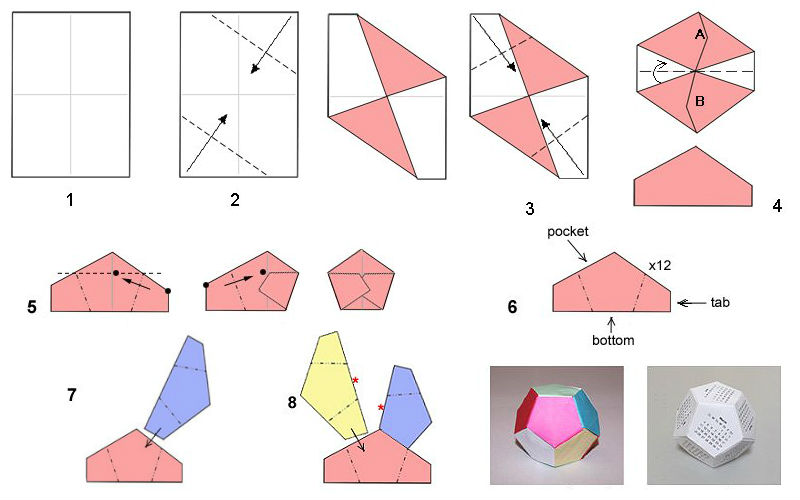
- Как сделать додекаэдр: инструкция по изготовлению
- Правильный додекаэдр — это многогранник, гранями которого являются двенадцать правильных пятиугольников, также являющийся одним из пяти правильных многогранников, которые называются Платоновыми телами.
- Страницы Главная страница.
- Сделать из бумаги многогранник — Икосаэдр очень просто в технике оригами из модулей Mitsunobu Sonobe.

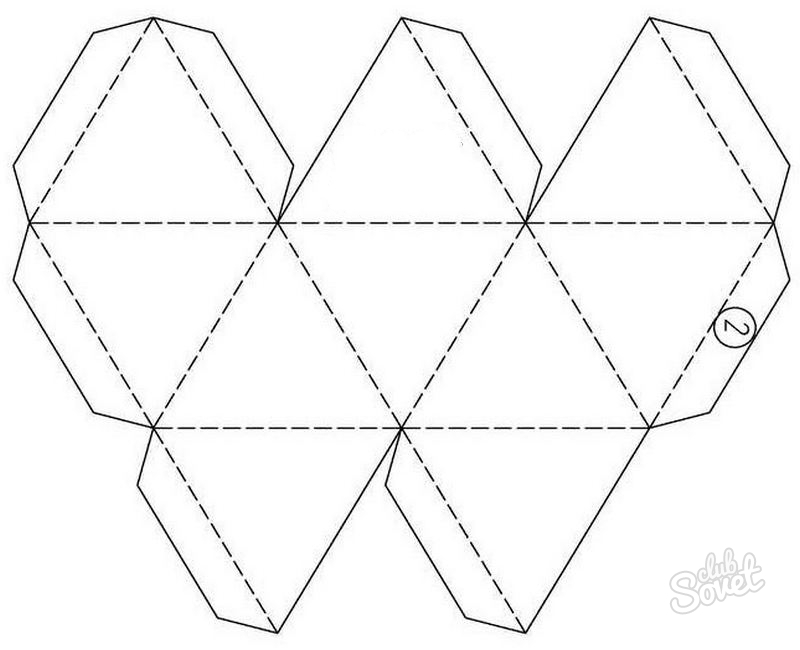








Гексаэдр куб, четырёхугольная призма, шестигранник — многогранник, каждая грань которого представляет собой квадрат. Также является одним из пяти правильных многогранников Платоновых тел. У куба 6 граней, 8 вершины и 12 рёбер. Двойственным многогранником куба является тоже октаэдр. Куб обладает октаэдрической симметрией. Правильный многогранник платоново тело — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий одной из пространственной симметрией тетраэдрический, октаэдрический или икосаэдрический.