Отношение равносильности это

равносильность
Равенство является интуитивно очевидным отношением: значение двух выражений одно и то же. При его формальном определении возникает разнобой. Теория множеств , по определению, считает два объекта то есть, два множества равными, если они состоят из одних и тех же элементов:. В теориях с типизацией объектов отношение равенства имеет смысл лишь между элементами одного типа попросту говоря, внутри определённого множества.





Два элемента эквивалентны в том и только том случае, если их классы эквивалентности совпадают, т. Указанные правила определяют обратные друг другу отображения, устанавливающие взаимно однозначное соответствие между множеством всех отношений эквивалентности на X X X и множеством всех разбиений на нём. Это соответствие имеет фундаментальный характер; его существование неформально может быть выражено фразой: «задать отношение эквивалентности на множестве — это то же самое, что задать его разбиение». Классами эквивалентности являются одноэлементные множества. Отношение эквивалентности на произвольном множестве X X X , отождествляющее все его элементы, т.
- Тождественно истинная формула
- Областью допустимых значений ОДЗ неравенства или уравнения называют множество всех значений переменной x x , при которых одновременно определены обе части неравенства или уравнения, т. Решить неравенство уравнение — это значит найти все числа a a , после подстановки которых, вместо x x получается верное числовое неравенство равенство , или доказать, что неравенство уравнение не имеет решений.
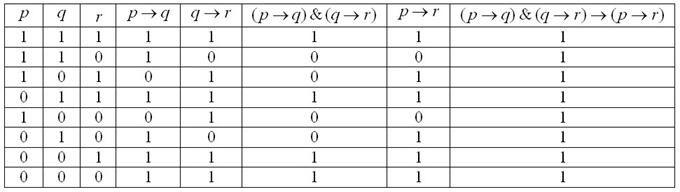
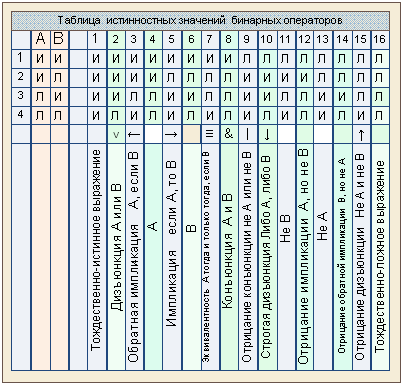
- Равносильность высказывания — это понятие из логики, которое относится к сравнению двух высказываний и определяет, являются ли они семантически эквивалентными. Одно высказывание считается равносильным другому, если они имеют одинаковую истинностную таблицу, то есть истинность каждого из них зависит от одних и тех же истинностных значений входных переменных.
- Число a называется корнем или решением уравнения 1 , если при подстановке этого числа в уравнение получается верное числовое равенство.









Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах. Вычисление криволинейного интеграла второго рода в случае выполнения условия независимости от формы.







